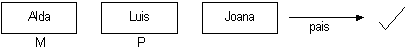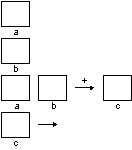Alma Homepage

Alma System (resumo em português)

·        Create a system able to extract the meaning of a program and to present it in a clear way using visual explanations of the program behaviour simulations.

·        Remove language and program dependencies

                       

Alma System: Design Goals

 

·        Build an integrated and easy to use environment

·        Avoid the need for any kind of change in the source code

·        Allow the selection of different views of the same program

·        Create a system as generic as possible in order to be used by different source languages

 

Alma System: Architecture

 

 

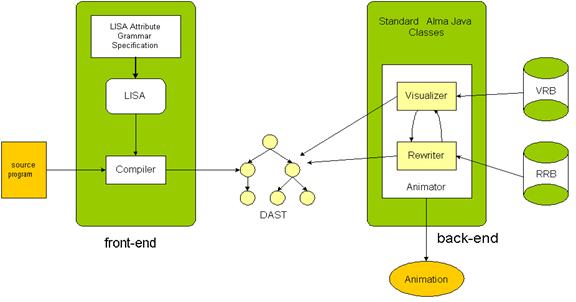
Input and Output of ALMA

 

·        INPUT – the specification of FE allows the user to map the conceptual elements of his language to the DAST nodes

·        OUTPUT – the BE works on that DAST using two bases of rules (visualizing rules and rewriting rules) and constructs the output – the animation.

 

Alma System: Internal Representation (DAST- Decorated Abstract Syntax Tree)

 

·        Structure of DAST nodes – name of the symbol, production identifier, set of attributes, children nodes, ... (that will represent names, types and values of the source program identifiers)

·        The set of symbols is pre-defined and the symbols that can be generated belong to the abstract grammar of the Alma

·        One node can represent different things depending on the source language but it must represent the same underlying semantics

·        These nodes are used on the BE rules definition (VRB and RRB)

 

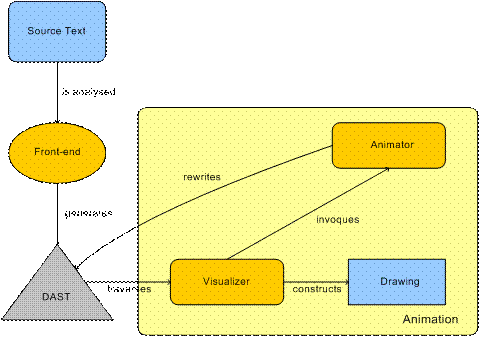
Alma System: Front-end

 

n      One FE for each language (grammar) that constructs the DAST using pre-defined methods in the semantic evaluation (the use of these methods depends on a mapping that associates concepts of the source program to DAST nodes)

 

Alma System: Back-end

 

n      Independent of the source language

n      It’s the same for all the FE’s

n      Implements the algorithm animation

n      Works over the DAST based on a set of visualizing rules (VRB) and a set of rewriting rules (RRB)

n      The animation is based on the internal representation of the source program

n      That internal representation has standard syntax formally specified by a grammar

n      The visualizing and rewriting mapping are easily specified

 

      

 

 

 

Animation Algorithm

 

Is divided into:

Tree walker visualizer

–         Traverses the tree applying the visualizing rules to the appropriate subtrees

–         Applies several (as many as possible) rules in one traversal

–         Produces the visualization of one state of the program

Tree walker rewriter

–         Traverses the tree but it applies only one rewriting rule (semantic or syntactic modification)

–         Then the tree will be ready to be visualized again

 

Visualizing rules

 

VRB: DAST ® set (condition ´ drawprod)

Vis_rule(ProdId) = <tree_pattern>,

                   (condition),

                   {drawing procedure}

<tree_pattern>=<root,child1,...,childn>

 

*      Note that it can be specified more then one rule for each production

 

Rewriting rules

 

RRB: DAST ® set(condition ´ newtree ´ attribsEval)

Rew_rule(ProdId) = <tree_pattern>,

                   (condition),

                   <newtree>,

                   {attribsEval}

 

*      Note that it can be specified more then one rule for each production

 

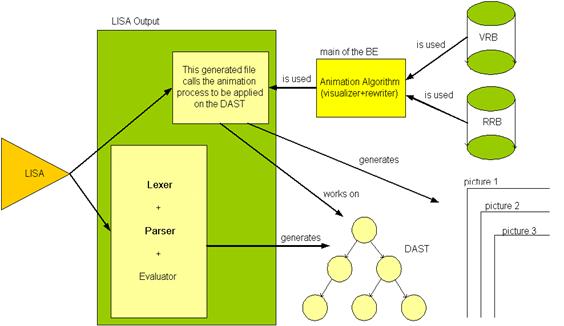
Reusing Lisa System in Alma Implementation

 

  • Lisa System is used to construct the FE for each new input language of Alma System.
  • Some of its Java classes and editors are used to edit and show the inputs and results of Alma.

 

 

Reusing LISA in BE of ALMA

 

 

The first example is a simple imperative language…

 

Source text…

 

a ? ;

b ? ;

let  c  =  a  +  b  ;

c  !  ;

 

FE construction

 

rule AlmaAxioma{

     PROG ::= STATS  compute {PROG.dast = mkroot(STATS.tree);};         

     }                            

rule STS {

     STATS ::= STAT \; STATS  compute {STATS[0].tree =  mkstats(STAT.tree,STATS[1].tree);}                                    

             | STAT \; compute {STATS.tree=STAT.tree;};

     }

rule STATEMENT {

     STAT ::=  let  VAR  =  EXP  compute {STAT.tree = mkassign(VAR.tree, EXP.tree);}

             | VAR  \?  compute {STAT.tree = mkread(VAR.tree);}

             | VAR  !  compute {STAT.tree = mkwrite(VAR.tree);};

     }

rule EXPR {

     EXP ::=  T #opad EXP  compute {EXP[0].tree = mkoper(T.tree,EXP[1].tree,#opad.value());}

            | T  compute {EXP.tree = T.tree;};

     }     

 

Generated DAST

 

 


                       

 

 

 

 

 

 

 

 

 

 

 

 

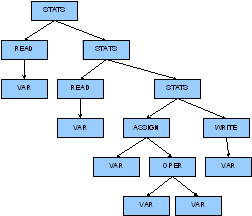
Generated Animation

           

 

With a new FE for a robot language and some new rewriting and visualizing rule we will get very different results….

We will  get a different abstraction level…

 

Source language grammar

 

robot → ini_pos moves

ini_pos → “xi =“ INT “yi =“ INT

moves →  moves mov

      |  mov

mov → dir nsteps

dir → DOWN | RIGHT | UP | LEFT

nsteps → INT

 

Source text

 

xi= 0

yi= 0

DOWN 3

RIGHT 7

UP 2

LEFT 4

 

Generated DAST

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 


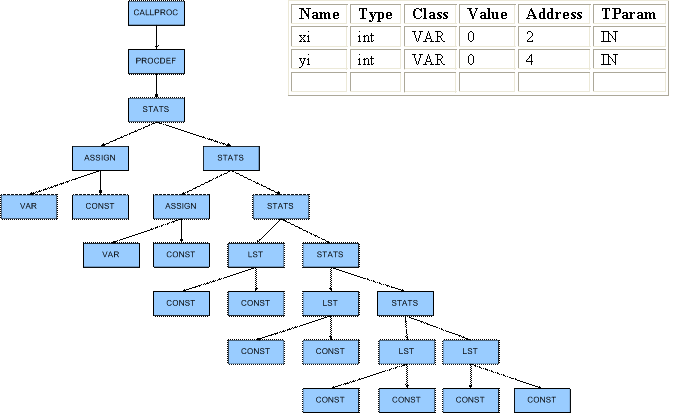
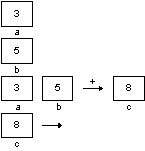
Rewriting Rules

 

rew_rule(lstmov) = <a:lst, b:const, c:const>,

                   (getvalue(b)!=NULL),

                   <a:lst, b: const, c: const>,

                   { x=getTableVal(xi);

                     y=getTableVal(yi);

                     calculate(x,y,getValue(b),getValue(c))

                     putTableVal(xi,x);

                     putTableVal(yi,y);}

 

rew_rule(passign) = <at:assign, a1: var, b: exp>,

                    (getValue(b)!=NULL),

                    <passign: at: assign, a2: var, b: exp>,

                    { setName(a2,getName(a1));

                      setValue(a2,getValue(b));}

 

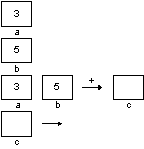
Visualising Rules

 

vis_rule(robot) = <a: procdef, b: stats>,

                  (),

                  <a:procdef, b:stats>,

                  {drawrobot(getValue(xi), getValue(yi))}

 

drawrobot(int x, int y){

          String fich = getImage(x,y);

          drawImage(“fich.gif”);

}

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 


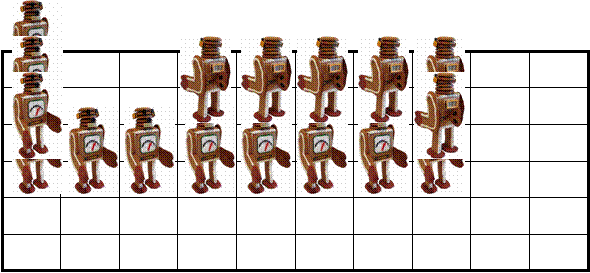
With a new FE for Prolog programs and using the same rules used in the first examples we will get the animation below….

 

Source program

 

mãe(alda,joana).

mãe(joana,joão).

pai(luis,pedro).

pai(luis joana).

pais(M,P,E) :- mae(M,E), pai(P,E).

 

 

Generated DAST

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 


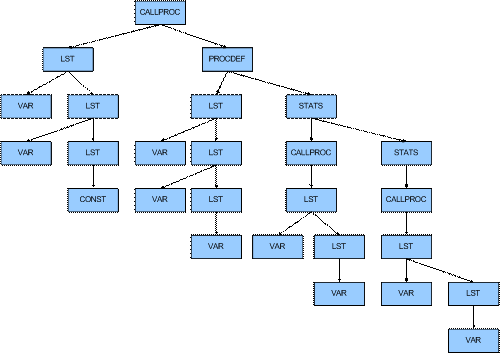
Image nº1

Image nº2

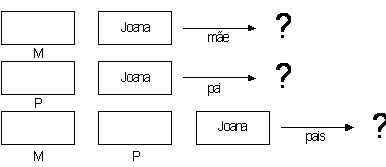
Image nº3

 

 

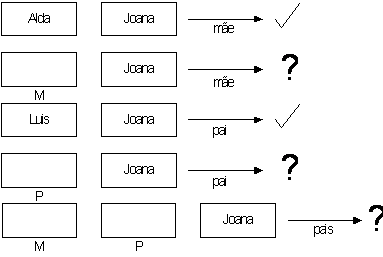
Image nº4

 

 

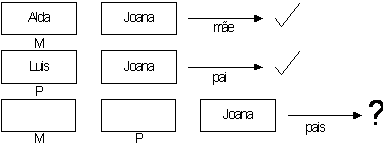
Image nº5